Introduction

One of the most prominent problems when we first started looking at averaging polls is that the best data we had to work with was from 2016, data that is known to be problematic. The original assumption was that we would create an exponential function that would intake data on a poll’s age, number and type of respondents e.g., likely vs. registered voters, and the quality of its polling company, then output a weight so that we could create a weighted average of all the polls. We would find these weights by trying out various regressions and finding which did the best job at predicting the outcome of the 2016 election based on the polls of the time. But as those polls were so far off the mark, how could we get any useful data from them? We would have no guarantee that the weights we came up with would be any good once applied to 2020 data.

So we took a step back and considered whether or not we even had to use an exponential function to begin with. We found little correlation between the quality of a poll’s company and the accuracy of its outcome, so we threw out that consideration entirely. We also found that while older polls were sometimes reliable and sometimes not for predicting an election, the very recent polls were almost always the closest. This inspired a new line of thought: what if, instead of performing a regression, we simply referred to the most recent polls? This thinking eventually resulted in the z-test model.

Aside from being a more accurate model with the old data than traditional regressions, the z-test model had several benefits. We no longer had to worry about accommodating for “convention bumps” in the polls, and if an event occurred that changed the political opinions of a significant number of people, our model would better reflect this change because it would not be affected by the out of date polls.

However, we adopted this model with caution. All of the other major political prediction models, as well as the older Oracle of Blair models, use the traditional regression method. And it is fairly counterintuitive that we can gain a more accurate result by completely throwing out information like older polls and reliability ratings.

Early Implementation and Development

The z-test model started as an excel spreadsheet and the portion of the sheet where we tested the model with Texas data can be seen below. We started by sorting all polls by weeks before the election and averaging the polls in each week. This value can be seen in the column ‘pred’, which shows the predicted 2-party vote percent for Hillary. Then, we copied over the numbers of respondents who favored clinton and the number of two party respondents in the week, so that we could calculate the p-hat pooled value. The p-hat pooled value was then calculated between the last two available weeks and stored in column ‘p-hat pooled’.

We then performed a two-tailed z-test between the current week’s average and the week before its averaging using the p-hat pooled value with the null hypothesis that the two weeks would be the same. The z-score was stored in column ‘z-score’ and the p-value in column ‘p-value’. Then, if p was less than 0.05 the difference between the two weeks was deemed significant.

The confusing part about the spreadsheet is that it was easier to work with values in terms of being not significant, so in column ‘non sig’ you will see FALSE when there is a change between the two weeks. Lastly, we used the judgment in ‘non sig’ to make an adjusted prediction for every week that either used the current week as the prediction (‘non sig’=FALSE) or took a weighted average with the previous week’s adjusted prediction where the current week was weighted twice as much as the previous (‘non sig’=TRUE).

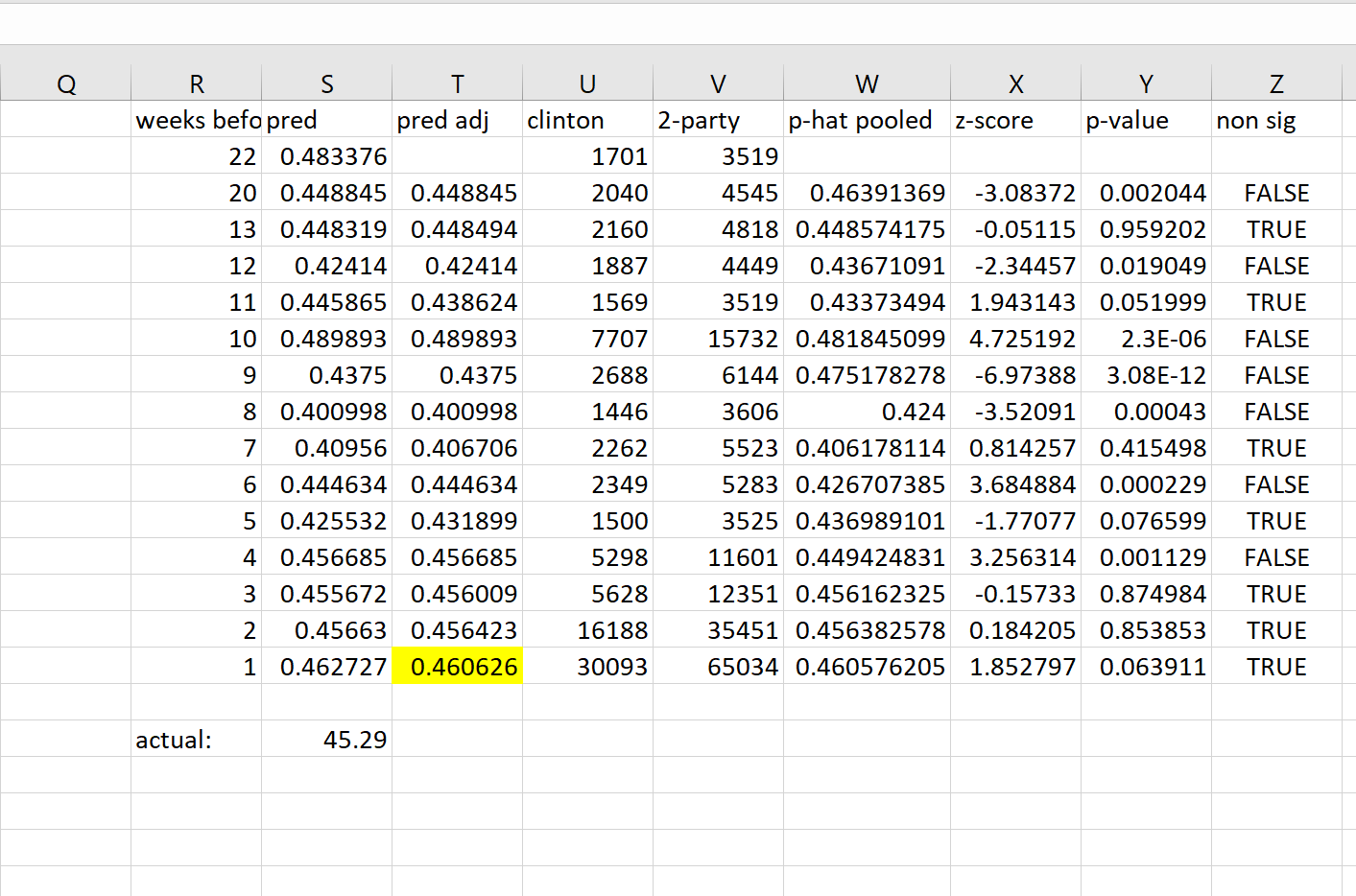Fig. 1 Excel spreadsheet for Texas with the first version of the Z-Test method

There are a couple interesting things to notice about this primitive spreadsheet version of the model. First is that averages were not rolling. The polls were taken in 7 day blocks that had no overlap of polls. This was a good starting point to test the idea, but could never work for the final version since the model needs to update every day, but the non-rolling polls could only be tested and updated once a week.

The next interesting thing is the averages we were taking for the weeks was actually a pooled value of the week since we simplified our formulas by just taking (Clinton respondents in week x)/(2-party respondents in week x) as the average in that week. This is very much a poor man’s version of the meta-analysis we ended up doing, and also could not have worked in the final model since it ignored the differing errors amongst the polls.

The last interesting thing is that there was a weight on the newer week. The idea behind this weight was that there was a chance that there had been a significant change in the population and that the test should have thrown out previous weeks, but did not (a false negative). To try and account for this we put a double weight on the newest week so that the effects of any false negative would be lessened and that double weights would not hurt true negatives since the population was hypothetically the same between the two weeks. However, the removal of this weight during later iterations had little effect, thus it was deemed unnecessary and potentially problematic, so it was eliminated in the final model.

Let's compare!

Let’s compare the regression model used in our 2018 Oracle of Blair to our current z-test model. Starting with the regression model, the first step is to first obtain the weights for each of the polls. The traditional method of calculating weights was to use an exponential. In 2018, the poll's relative values of the function: $$f(x) = e^{-t/30}$$ where t is the number of days between the election and the day the poll finished, determined its weight. Therefore, if there are m polls in a district and the ath poll is from \(t_a\) days before the election, it will have weight \(w_a\) according the the equation: $$W_a=\frac{e^{-t_a/30}}{\sum\limits_{i=1}^m e^{-t_i/30}}$$

We’ll focus our comparison on two key swing states: Florida and Texas.

The Oracle’s current prediction for Florida is that 49.3% of the two-party vote will go to Trump. The polling average predicted by the regression model is 48.5%, which when averaged with the priors (as described in our methodology section) gives a prediction of 48.7%.

As for Texas, the Oracle’s current prediction is that 50.2% of the two-party vote will go to Trump. If we had used the traditional regression model, the poll average would have been 51% and the final prediction would be 51.34%.

These may not seem like large differences, but for elections this close, a percentage point or two can be a big deal in the chances of winning. For example, if we were using our old model with Texas, we would give Trump almost a 62% chance of winning, a much less close race than we are currently predicting. Similarly, in Florida, we would give Trump less than a 42% chance of winning.

The fact that the Z-test model predicts closer races in both of these states is quite intriguing, especially because it shows a Republican-leaning state shifting to the left and a Democratic-leaning state shifting to the right. This means that the earlier polls excluded by the Z-test model but included by the regression model must be less competitive than the recent ones, suggesting that the race has, if anything, become closer in the past few weeks (at least in these states).

So yes, the change in model does make a difference, if not an extraordinarily dramatic one. Is it perfect? Well, of course there’s still room for improvement. For example, when calculating the portion of the standard deviation due to polling variation, it would be more accurate to count the number of respondents in the polls rather than just the number of polls. But overall, we believe that the Z-test model is a better predictor than a traditional regression model. We’ll just have to wait and see if our confidence was well founded.